Large Language Models (LLM) have recently been proven as reliable tools for improving productivity in lots of areas reminiscent of programming, content creation, text evaluation, web search, and distance learning.
The Impact of Large Language Models on Users’ Privacy
Despite the appeal of LLMs, privacy concerns persist surrounding user queries which can be processed by these models. On the one hand, leveraging the facility of LLMs is desirable, but alternatively, there’s a risk of leaking sensitive information to the LLM service provider. In some areas, reminiscent of healthcare, finance, or law, this privacy risk is a showstopper.
One possible solution to this problem is on-premise deployment, where the LLM owner would deploy their model on the client’s machine. That is nonetheless not an optimal solution, as constructing an LLM may cost hundreds of thousands of dollars (4.6M$ for GPT3) and on-premise deployment runs the chance of leaking the model mental property (IP).
Zama believes you possibly can get the perfect of each worlds: our ambition is to guard each the privacy of the user and the IP of the model. On this blog, you’ll see find out how to leverage the Hugging Face transformers library and have parts of those models run on encrypted data. The entire code will be present in this use case example.
Fully Homomorphic Encryption (FHE) Can Solve LLM Privacy Challenges
Zama’s solution to the challenges of LLM deployment is to make use of Fully Homomorphic Encryption (FHE) which enables the execution of functions on encrypted data. It is feasible to realize the goal of protecting the model owner’s IP while still maintaining the privacy of the user’s data. This demo shows that an LLM model implemented in FHE maintains the standard of the unique model’s predictions. To do that, it’s vital to adapt the GPT2 implementation from the Hugging Face transformers library, reworking sections of the inference using Concrete-Python, which enables the conversion of Python functions into their FHE equivalents.
Figure 1 shows the GPT2 architecture which has a repeating structure: a series of multi-head attention (MHA) layers applied successively. Each MHA layer projects the inputs using the model weights, computes the eye mechanism, and re-projects the output of the eye right into a latest tensor.
In TFHE, model weights and activations are represented with integers. Nonlinear functions should be implemented with a Programmable Bootstrapping (PBS) operation. PBS implements a table lookup (TLU) operation on encrypted data while also refreshing ciphertexts to permit arbitrary computation. On the downside, the computation time of PBS dominates the considered one of linear operations. Leveraging these two varieties of operations, you possibly can express any sub-part of, or, even the complete LLM computation, in FHE.
Implementation of a LLM layer with FHE
Next, you’ll see find out how to encrypt a single attention head of the multi-head attention (MHA) block. You can too find an example for the complete MHA block on this use case example.
Figure 2. shows a simplified overview of the underlying implementation. A client starts the inference locally as much as the primary layer which has been faraway from the shared model. The user encrypts the intermediate operations and sends them to the server. The server applies a part of the eye mechanism and the outcomes are then returned to the client who can decrypt them and proceed the local inference.
Quantization
First, in an effort to perform the model inference on encrypted values, the weights and activations of the model should be quantized and converted to integers. The best is to make use of post-training quantization which doesn’t require re-training the model. The method is to implement an FHE compatible attention mechanism, use integers and PBS, after which examine the impact on LLM accuracy.
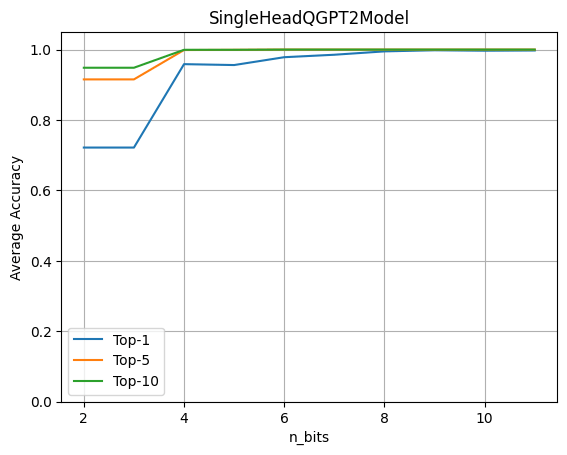
To guage the impact of quantization, run the complete GPT2 model with a single LLM Head operating over encrypted data. Then, evaluate the accuracy obtained when various the variety of quantization bits for each weights and activations.
This graph shows that 4-bit quantization maintains 96% of the unique accuracy. The experiment is finished using a data-set of ~80 sentences. The metrics are computed by comparing the logits prediction from the unique model against the model with the quantized head model.
Applying FHE to the Hugging Face GPT2 model
Constructing upon the transformers library from Hugging Face, rewrite the forward pass of modules that you must encrypt, in an effort to include the quantized operators. Construct a SingleHeadQGPT2Model instance by first loading a GPT2LMHeadModel after which manually replace the primary multi-head attention module as following using a QGPT2SingleHeadAttention module. The entire implementation will be found here.
self.transformer.h[0].attn = QGPT2SingleHeadAttention(config, n_bits=n_bits)
The forward pass is then overwritten in order that the primary head of the multi-head attention mechanism, including the projections made for constructing the query, keys and value matrices, is performed with FHE-friendly operators. The next QGPT2 module will be found here.
class SingleHeadAttention(QGPT2):
"""Class representing a single attention head implemented with quantization methods."""
def run_numpy(self, q_hidden_states: np.ndarray):
q_x = DualArray(
float_array=self.x_calib,
int_array=q_hidden_states,
quantizer=self.quantizer
)
mha_weights_name = f"transformer.h.{self.layer}.attn."
head_0_indices = [
list(range(i * self.n_embd, i * self.n_embd + self.head_dim))
for i in range(3)
]
q_qkv_weights = ...
q_qkv_bias = ...
q_qkv = q_x.linear(
weight=q_qkv_weights,
bias=q_qkv_bias,
key=f"attention_qkv_proj_layer_{self.layer}",
)
q_qkv = q_qkv.expand_dims(axis=1, key=f"unsqueeze_{self.layer}")
q_q, q_k, q_v = q_qkv.enc_split(
3,
axis=-1,
key=f"qkv_split_layer_{self.layer}"
)
q_y = self.attention(q_q, q_k, q_v)
return self.finalize(q_y)
Other computations within the model remain in floating point, non-encrypted and are expected to be executed by the client on-premise.
Loading pre-trained weights into the GPT2 model modified in this fashion, you possibly can then call the generate method:
qgpt2_model = SingleHeadQGPT2Model.from_pretrained(
"gpt2_model", n_bits=4, use_cache=False
)
output_ids = qgpt2_model.generate(input_ids)
For instance, you possibly can ask the quantized model to finish the phrase ”Cryptography is a”. With sufficient quantization precision when running the model in FHE, the output of the generation is:
“Cryptography is an important a part of the safety of your computer”
When quantization precision is just too low you’re going to get:
“Cryptography is a terrific solution to learn concerning the world around you”
Compilation to FHE
You’ll be able to now compile the eye head using the next Concrete-ML code:
circuit_head = qgpt2_model.compile(input_ids)
Running this, you will note the next print out: “Circuit compiled with 8 bit-width”. This configuration, compatible with FHE, shows the utmost bit-width vital to perform operations in FHE.
Complexity
In transformer models, essentially the most computationally intensive operation is the eye mechanism which multiplies the queries, keys, and values. In FHE, the fee is compounded by the specificity of multiplications within the encrypted domain. Moreover, because the sequence length increases, the variety of these difficult multiplications increases quadratically.
For the encrypted head, a sequence of length 6 requires 11,622 PBS operations. This can be a first experiment that has not been optimized for performance. While it may possibly run in a matter of seconds, it might require quite numerous computing power. Fortunately, hardware will improve latency by 1000x to 10000x, making things go from several minutes on CPU to < 100ms on ASIC once they can be found in a couple of years. For more details about these projections, see this blog post.
Conclusion
Large Language Models are great assistance tools in a wide selection of use cases but their implementation raises major issues for user privacy. On this blog, you saw a primary step toward having the entire LLM work on encrypted data where the model would run entirely within the cloud while users’ privacy could be fully respected.
This step includes the conversion of a particular part in a model like GPT2 to the FHE realm. This implementation leverages the transformers library and means that you can evaluate the impact on the accuracy when a part of the model runs on encrypted data. Along with preserving user privacy, this approach also allows a model owner to maintain a serious a part of their model private. The entire code will be present in this use case example.
Zama libraries Concrete and Concrete-ML (Remember to star the repos on GitHub ⭐️💛) allow straightforward ML model constructing and conversion to the FHE akin to with the ability to compute and predict over encrypted data.
Hope you enjoyed this post; be happy to share your thoughts/feedback!