NVIDIA cuOpt is a GPU-accelerated optimization engine designed to deliver fast, high-quality solutions for giant, complex decision-making problems. Mixed integer programming (MIP) is a method for solving problems. It could be modeled by a set of linear constraints, with a number of the variables capable of assume only integer values. The varieties of problems that will be modeled as MIP are quite a few and include areas reminiscent of production planning, supply chain, transportation, scheduling, and finance.
NVIDIA cuOpt is a GPU-accelerated solver built to deliver low-latency, high-quality optimization for giant, constraint-heavy problems. At its core, cuOpt uses mixed-integer programming (MIP), which formulates decisions as linear constraints with each continuous and integer variables. This makes it well-suited for domains like supply-chain network optimization, routing and dispatch, workforce and task scheduling, production planning, and quantitative finance.
Accelerated primal heuristics for MIP solvers are algorithms that deliver high-quality, feasible solutions without exhaustively searching your complete solution space. They’re needed for 2 reasons. First, many real-world MIP problems are too large or time-sensitive for traditional solvers to search out answers in time. Second, they permit pruning the search space of a Branch and Certain algorithm. Accelerated heuristics reduce solve times by utilizing parallelism and smarter search strategies, enabling businesses to reply to disruptions and make low-latency decisions.
This post explains how NVIDIA cuOpt uses GPU acceleration to deliver high-quality solutions to MIP problems through primal heuristics, enabling the invention of recent solutions for 4 open instances from the MIPLIB benchmark set: liu.mps, neos-3355120-tarago.mps, polygonpack4-7.mps, and bts4-cta.mps. The demonstrated results showcase substantial improvements in solution quality and the variety of feasible solutions in comparison with leading open-source CPU solvers.
Why fast, high-quality solutions matter for large-scale MIPs
A MIP is a component of a category of NP-hard problems, meaning that no known algorithm can solve all such problems quickly within the worst case. Nonetheless, despite their NP-hardness, industrial MIP solvers routinely deliver optimal solutions for a lot of large instances.
But certain problems remain intractable or require prolonged computation times. On condition that MIP models real-world problems and infrequently maps on to operational costs, it has been a longstanding goal—dating back to the mid-Twentieth century—to develop algorithms able to efficiently solving increasingly large and complicated instances. Significant theoretical and computational breakthroughs have been made since then, including the branch and certain algorithm, cutting planes, primal heuristics just like the feasibility pump, and, more recently, parallel processing.
Real-world problems are typically dynamic, with inputs that change over time. This requires solvers to make use of iterative and incremental approaches, making speed essential at every step. Time-critical MIPs include flexible job-shop scheduling and variants, lot sizing, and airline or railway crew scheduling. Consequently, in cuOpt, significant effort has been dedicated to developing primal heuristics for the invention of high-quality solutions inside a temporary timeframe— often faster than another open-source solver.
How you can get high-quality feasible solutions for MIPs
Some of the successful primal heuristics up to now is the feasibility pump (FP), with recent papers based on the thought emerging yearly. The predominant idea is comparatively easy: iterate between projections onto the feasible region and rounding variables that remain fractional using domain propagation.
We began by improving the present algorithms to maximise GPU performance and address two predominant bottlenecks of the FP algorithm:
- The projection is modeled as a Linear Programming problem.
- Domain Propagation after the projection
We observed that the precision of the projection within the FP algorithm isn’t that vital, as we obtained similar results even with lower precision. This gave us the concept a first-order method may very well be used as an alternative of the simplex algorithm, and fortunately, the PDLP(Primal-Dual hybrid gradient) was already implemented within the cuOpt framework.
We warm-start the PDLP algorithm with the primal and dual solutions of the previous projection. Using PDLP within the FP, in addition to at the foundation node, enabled us to iterate much faster and solve larger problems more effectively. To tackle the second bottleneck, we implemented a GPU version of the domain propagation algorithm with significant improvements, reminiscent of bulk rounding and dynamic variable rating. After removing these bottlenecks, our focus shifted to removing cycling inside FP.
Cycling is the issue of repeating steps, and is normally solved by introducing randomness to explore different regions of the search space. As an alternative, we opted for using the Local-MIP algorithm to interrupt the cycle and, at the identical time, improve the target. To do it efficiently, Local-MIP was implemented on the GPU, outperforming the usual CPU version.
We also added the target cutoff at every iteration and located a brand new best-feasible solution. We’ve published a paper detailing this.
These improvements led to a complicated primal heuristic for locating feasible solutions. The next table shows a comparison of our method with a recent FP variant and the Local-MIP by way of the variety of feasible solutions (average over 3 runs) and the target gap (normalized difference between the optimal solution and the one found by our heuristics):
| Method | Avg. # Feasible | Primal gap |
| Fix and propagate portfolio default | 193.8 | 0.66 |
| Local-MIP | 188.67 | 0.46 |
| GPU Local-MIP | 205 | 0.41 |
| GPU Prolonged FP with nearest rounding | 220 | 0.23 |
| GPU Prolonged FP with Fix and Propagate | 220.67 | 0.22 |
Along with these enhancements, we introduced three novel evolutionary algorithms to further refine the model. The evolutionary algorithms, applied upon detection of stagnation, effect a further 3% reduction within the primal gap. The incorporation of an easy Branch and Certain approach (excluding cutting planes) with diving threads and a subMIP-based Evolutionary Algorithm provided an excellent greater degree of improvement. We now proceed to check this method with the widely used open-source solvers:
MIP solvers benchmarks
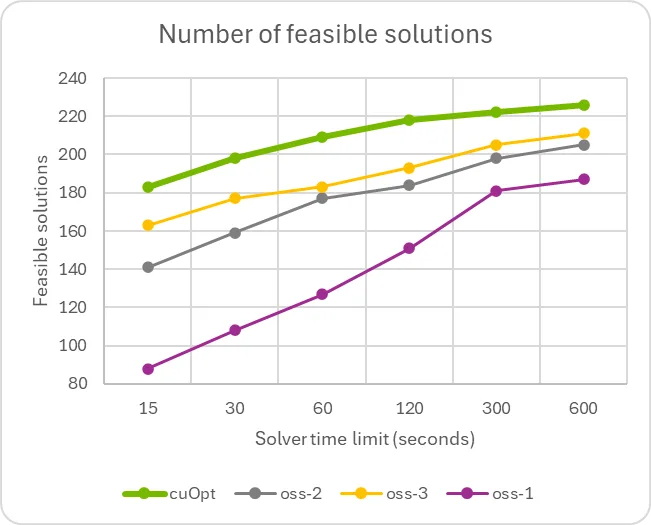

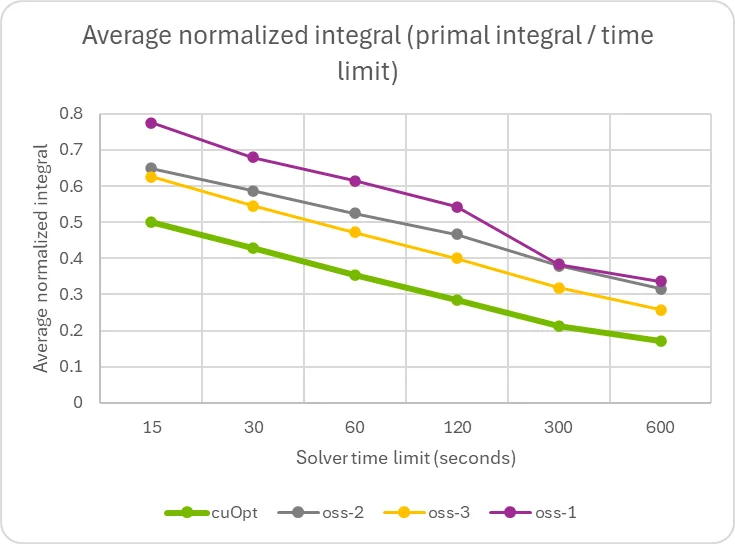

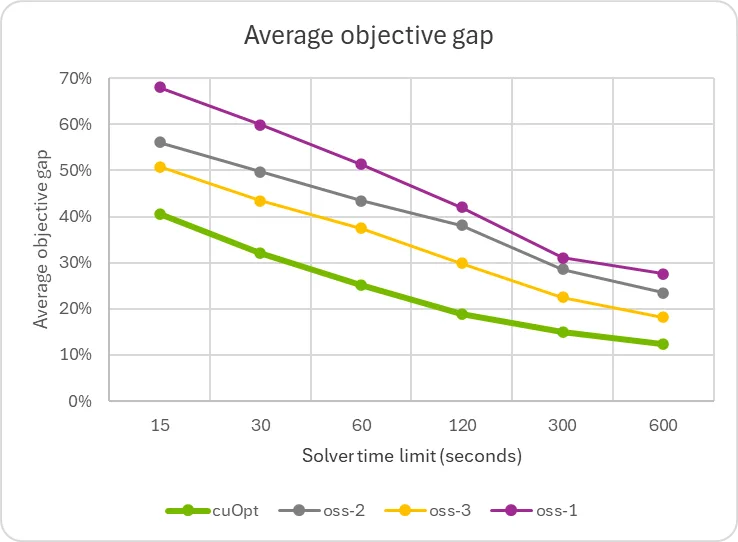

The graphs show a considerable speedup in comparison with solvers that incorporate sophisticated cutting plane algorithms and problem-specific methodologies. This means potential for further improvement, in addition to the opportunity of augmenting any existing solver with the GPU-accelerated primal heuristics detailed previously.
How GPUs make MIP solving practical
Fast, feasible MIP solving plays a critical role in decision intelligence pipelines. When integrated with systems reminiscent of Palantir Ontology and NVIDIA Nemotron reasoning agents, it enables scenario generation and evaluation across many operational models in parallel. The open source GPU-accelerated MIP solver in cuOpt computes feasible solutions inside seconds, enabling downstream agents to simulate alternatives and re-optimize plans as conditions change. This capability turns static optimization right into a continuous feedback process for supporting adaptive decision making at scale.
Start with the MIP heuristics solver
MIP heuristics offer fast and feasible solutions without exhaustively exploring the issue space. This permits organizations to quickly test alternatives and reply to real-world disruptions, reminiscent of port delays, equipment failures, or sudden demand spikes. NVIDIA cuOpt uses GPU acceleration to make these heuristics practical at scale, producing faster solutions, reducing objective gaps, and enabling continuous, adaptive decision-making pipelines. Explore the NVIDIA cuOpt GitHub to experiment and take a look at out examples of MIP use cases on your optimization problems.
